Теоретична частина
Конструкція робота «Robot Arm»:
Загальний вид робота 6DoIt Mobile Robot Arm (6DMRA) представлений на рис.5. Його кінематичну схему показано на рис.6.

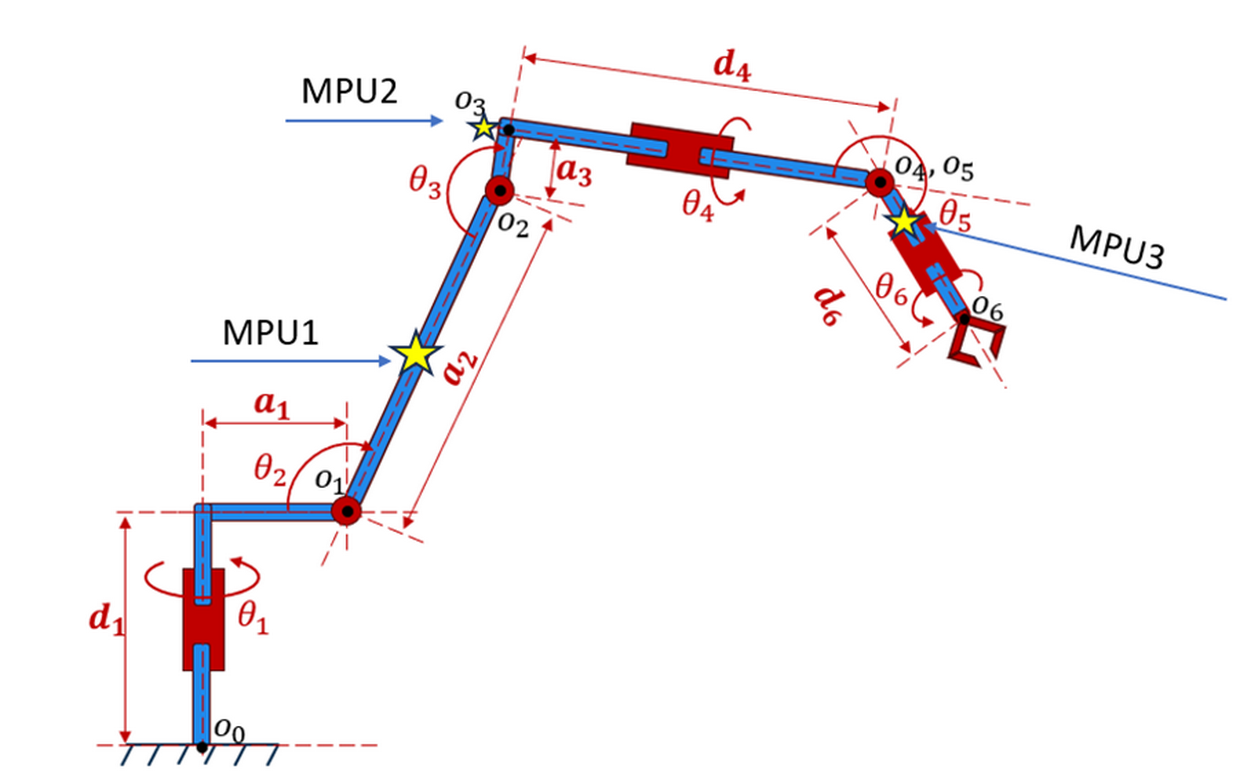
6DOF DoIt Mobile Robot Arm є меншою версією промислових роботів з 6 ступенями свободи. Цей невеликий маніпулятор вагою до 1 кг з максимальним навантаженням до 0.5 кг може бути вмонтований в тверду поверхню, встановлений на стіл або на спеціальне шасі. База робота має можливість розвороту до 180°.
Робот складається з шести кінематичних пар. Кожна кінематична пара має свої геометричні розміри, що визначаються параметрами \(d_i\) та \(a_i\), а кут обертання рухливої ланки – \(θ_i\). Кожна вісь обертання позначена буквою \(0_i\). Геометричні розміри маніпулятора представлено у табл.1.
| Вісь | Кут з’єднання (θі) | Скручування ланки (αі) | Довжина ланки (aі) (mm) | Зсув ланки (dі) (mm) |
|---|---|---|---|---|
| 1 | θ1 | -90° | 45 | 75 |
| 2 | θ2 | 0° | 115 | 0 |
| 3 | θ1 | -90° | 20 | 0 |
| 4 | θ4 | 90° | 0 | 130 |
| 5 | θ5 | -90° | 0 | 0 |
| 6 | θ6 | 0° | 0 | 50 |
Робоча зона робота-маніпулятора в опорній площині визначається внутрішнім і зовнішнім радіусом робочої поверхні. Внутрішній радіус робочої поверхні становить 65 мм, зовнішній – 340 мм.
МЕТОД ДЕНАВІТА-ХАРТЕНБЕРГА (DENAVIT-HARTENBERG METHOD)
Кожне кінематичне зчленування (кінематична пара) робота 6DOF є обертальним і має одну степінь свободи руху. Рух рухливої ланки зчленування визначається так званою узагальненою координатою – кутом обертання (повороту) \(θ_i\) (рис.6).
При русі маніпулятора в робочій зоні робота узагальнені координати кожного зчленування змінюються, формуючи траєкторію руху хвату. Маючи шість зчленувань маніпулятора, робот 6DOF може приймати різні геометричні конфігурації ланок при заданій точці позиціонування хвату. Тому важливо вміти визначати абсолютні координати положення ланок для контролю геометричної конфігурації маніпулятора у відповідності до заданої.
Точка позиціонування хвату \(0_6\) визначається в системі координат \((x_0, y_0, z_0 )\), що розташовується у точці \(0_0\) початку коордитат (рис.6).
У випадку, коли абсолютні координати ланок відомі, положення хвату визначається однозначно у системі координат \((x_0, y_0, z_0 )\). Таким чином, вирішується пряма задача кінематики: розрахунок координат положення і орієнтації системи координат, що пов’язана зі схватом або робочим інструментом, при заданому наборі узагальнених координат маніпулятора. З цією метою реалізується метод Денавіта-Хартенберга, який має наступні кроки:
- Прив’язка систем координат до зчленувань маніпулятора (Binding of coordinate systems to links).
- Визначення параметрів ланок і зчленувань (Determination of parameters of links and joints).
- Побудова однорідних матриць перетворення (Construction of homogeneous transformation matrices).
Прив’язка систем координат до зчленувань маніпулятора. Для прив’язки систем координат до кожного зчленування необхідно виконати наступні правила:
- Встановити маніпулятор у нульове (початкове положення).
- Вісь \(z_i\) має співпадати з віссю обертання або віссю поступального руху \((i+1)-ї\) ланки.
- Вісь \(x_i\) має бути перпендикулярною осі \(z_{(i-1)}\) \((i-1)-ї\) ланки і перетинати цю вісь. Вісь \(x_0\) вибирається довільно.
- Вісь \(y_i\) є векторним множенням \(\overrightarrow{y}_i=\overrightarrow{z}_i × \overrightarrow{x}_i\) і створює праву систему координат.
З врахуванням цих правил для робота DMRA маємо наступну орієнтацію систем координат зчленувань (рис.7).
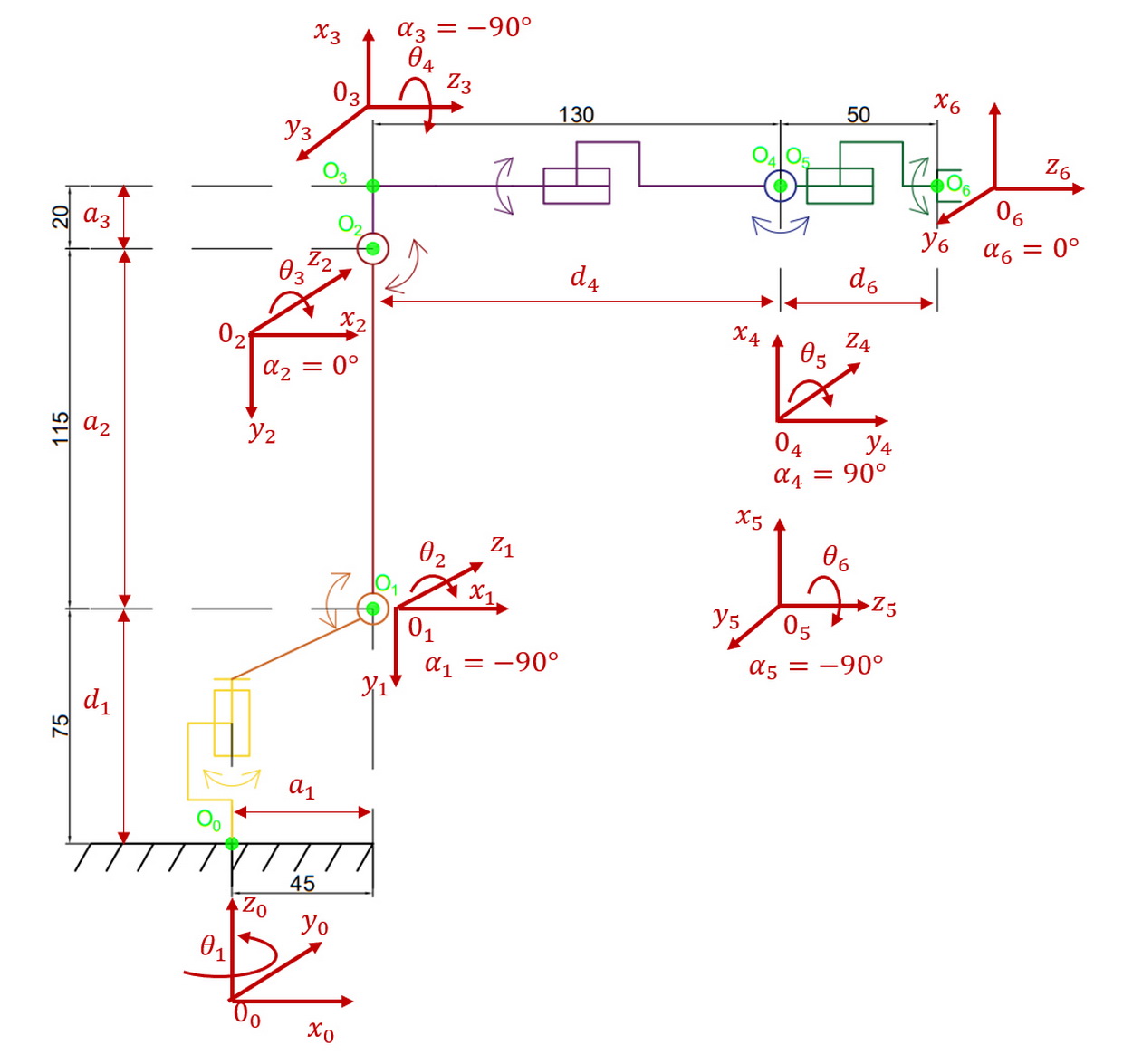
Визначення параметрів ланок і зчленувань. Для ланок і зчленувань маніпулятора робота користуються наступними параметрами Денавіта-Хартенберга:
\(θ_i\) – приєднаний кут, на який необхідно повернути вісь \(x_{(i-1)}\) навколо осі \(z_{(i-1)}\), щоб вона стала співнаправленою з віссю \(x_i\) (напрям обертання визначається за правилом правої руки);
\(d_i\) – відстань між точкою перетину осі \(z_{(i-1)}\) з віссю \(x_i\) і початком \((i-1)-ї\) системи координат, відлічена вздовж осі \(z_{(i-1)}\);
\(a_i\) – лінійне переміщення - відстань між точкою перетину осі \(z_{(i-1)}\) з віссю \(x_i\) і початком \((i)-ої\) системи координат, відраховане по осі \(x_i\), тобто найкоротша відстань між осями \(z_{(i-1)}\) і \(z_i\);
\(α_{(i)}\) – кутове зміщення - кут, на який необхідно повернути вісь \(z_{(i-1)}\) навколо осі \(x_i\), щоб вона стала співнаправленою з віссю \(z_i\) (напрям обертання визначається за правилом правої руки).
Параметри \(a_i\) і \(α_i\) завжди постійні для всіх кінематичних схем і визначаються конструкцією маніпуляторів. Що стосується інших параметрів \(d_i\) і \(θ_i\), то серед них лише один параметр постійний, а інший змінний, залежно від типу зчленування: при обертальному русі кут \(θ_i\) є змінним, параметр \(d_i\) є постійним, при поступальному – навпаки.
Для визначення параметрів Денавіта-Хартенберга користуються наступним алгоритмом:
- Обертання \((i-1)\) системи навколо осі \(z_{(i-1)}\) за годинниковою стрілкою (якщо дивитися з точки \(0_{(i-1)}\)) на кут \(θ_i\) до тих пір, поки вісь \(x_{(i-1)}\) не стане паралельною й однонаправленою до осі \(x_i\).
- Зсув повернутої \((i-1)-ої\) системи вздовж осі \(z_{(i-1)}\) на величину \(d_i\) до суміщення осі \(x_{(i-1)}\) з віссю \(x_i\).
- Зсув системи \((i-1)\) вздовж осі \(x_i\) на значення \(a_i\) до тих пір, поки точки початку координат систем \((i-1)\) і \((i)\) не збігаються.
- Поворот \((i-1)-ої\) системи навколо осі \(x_i\) за годинниковою стрілкою (якщо дивитися з точки \(0_i\)) на кут \(α_i\) до тих пір, поки вісь \(z_{(i-1)}\) не буде суміщена з віссю \(z_i\).
В результаті виконання наведеного алгоритму параметри ланок і зчленувань робота DMRA є наступними (табл.1).
Побудова однорідних матриць перетворення. Кожна однорідна матриця перетворень (трансферна матриця) ставить у відповідність координати \(i-ї\) ланки у \(i-й\) системі координат \((x_i, y_i, z_i)\) відносно координат цієї ланки у \(i-1-й\) системі координат \((x_{(i-1)}, y_{(i-1)}, z_{(i-1)})\)
| \begin{equation*} \left| \begin{array}{c} x_{i-1}\\ y_{i-1}\\ z_{i-1}\\ 1 \end{array} \right| = T_{i-1, i} \cdot \left| \begin{array}{c} x_{i}\\ y_{i}\\ z_{i}\\ 1 \end{array} \right|, \end{equation*} | (1) |
| \begin{equation*} T_{i-1, i} = \left| \begin{array}{cccc} c(θ_{i}) & -s(θ_{i})c(α_{i}) & s(θ_{i})s(α_{i}) & a_{i}c(θ_{i})\\ s(θ_{i}) & c(θ_{i})c(α_{i}) & -c(θ_{i})s(α_{i}) & a_{i}s(θ_{i})\\ 0 & s(α_{i}) & c(α_{i}) & d_i \\ 0 & 0 & 0 & 1 \end{array} \right|. \end{equation*} | (2) |
З урахуванням табл.1 і формул (1) та (2) маємо для кожного зчленування наступні трансферні матриці
| \begin{equation*} \left| \begin{array}{c} x_{0}\\ y_{0}\\ z_{0}\\ 1 \end{array} \right| = \left| \begin{array}{cccc} c(θ_{1}) & 0 & -s(θ_{1}) & a_{1}c(θ_{1})\\ s(θ_{1}) & 0 & c(θ_{1}) & a_{1}s(θ_{1})\\ 0 & 1 & 0 & d_1 \\ 0 & 0 & 0 & 1 \end{array} \right| \cdot \left| \begin{array}{c} x_{1}\\ y_{1}\\ z_{1}\\ 1 \end{array} \right|. \end{equation*} | (3) |
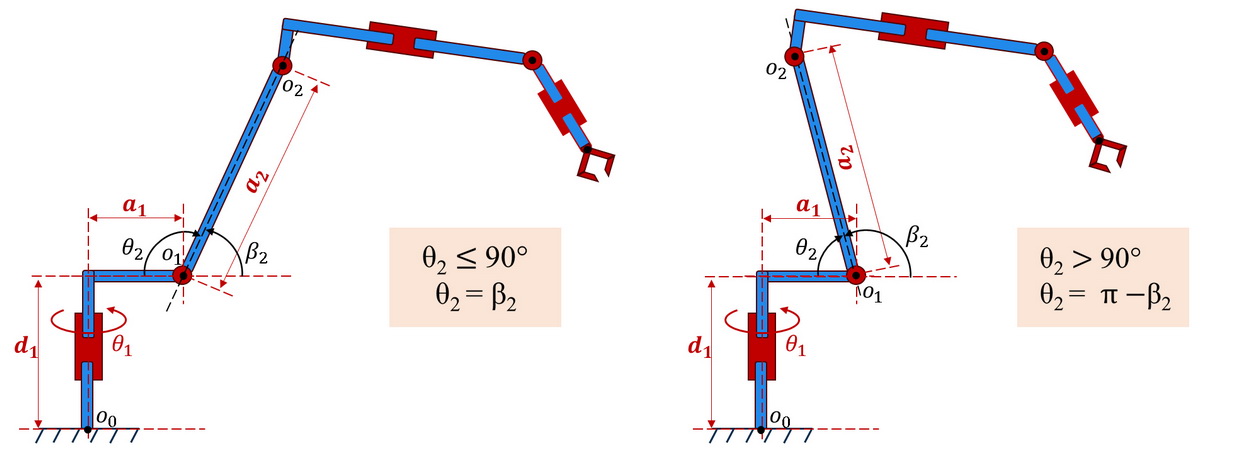
| \begin{equation*} \left| \begin{array}{c} x_{1}\\ y_{1}\\ z_{1}\\ 1 \end{array} \right| = \left| \begin{array}{cccc} c(θ_{2}) & -s(θ_{2}) & 0 & a_{2}c(θ_{2})\\ s(θ_{2}) & c(θ_{2}) & 0 & a_{2}s(θ_{2})\\ 0 & 0 & 1 & d_1 \\ 0 & 0 & 0 & 1 \end{array} \right| \cdot \left| \begin{array}{c} x_{2}\\ y_{2}\\ z_{2}\\ 1 \end{array} \right|, (рис.8), \end{equation*} | (4) |
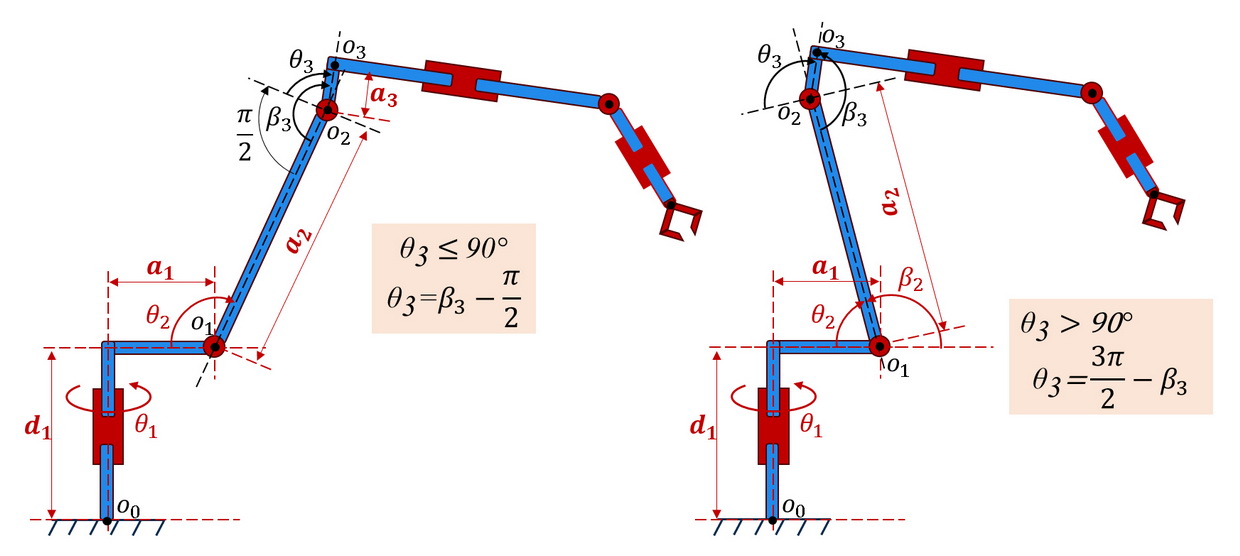
| \begin{equation*} \left| \begin{array}{c} x_{2}\\ y_{2}\\ z_{2}\\ 1 \end{array} \right| = \left| \begin{array}{cccc} c(θ_{3}) & 0 & -s(θ_{3}) & a_{3}c(θ_{3})\\ s(θ_{3}) & 0 & c(θ_{3}) & a_{3}s(θ_{3})\\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right| \cdot \left| \begin{array}{c} x_{3}\\ y_{3}\\ z_{3}\\ 1 \end{array} \right|, (рис.9), \end{equation*} | (5) |
| \begin{equation*} \left| \begin{array}{c} x_{4}\\ y_{4}\\ z_{4}\\ 1 \end{array} \right| = \left| \begin{array}{cccc} c(θ_{5}) & 0 & -s(θ_{5}) & 0\\ s(θ_{5}) & 0 & c(θ_{5}) & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right| \cdot \left| \begin{array}{c} x_{5}\\ y_{5}\\ z_{5}\\ 1 \end{array} \right|, (рис.10), \end{equation*} | (6) |
| \begin{equation*} \left| \begin{array}{c} x_{5}\\ y_{5}\\ z_{5}\\ 1 \end{array} \right| = \left| \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & d_6 \\ 0 & 0 & 0 & 1 \end{array} \right| \cdot \left| \begin{array}{c} x_{6}\\ y_{6}\\ z_{6}\\ 1 \end{array} \right|. \end{equation*} | (7) |
Використовуючи формули (3)...(7) можна отримувати координати \(i-ї\) ланки маніпулятора \((x_{(0,i)}, y_{(0,i)}, z_{(0,i)})\) в системі координат \((x_0, y_0, z_0)\), якщо відомі координати цієї ланки у системі координат \((x_i, y_i, z_i)\) та абсолютні координати переміщень \(θ_i (i=0...i)\) усіх ланок включно до \(i-ї\).
| \begin{equation*} \left| \begin{array}{c} x_{0,1}\\ y_{0,1}\\ z_{0,1}\\ 1 \end{array} \right| = T_{0, i} \cdot \left| \begin{array}{c} x_{i}\\ y_{i}\\ z_{i}\\ 1 \end{array} \right| = T_{0, 1} \cdot T_{1, 2} \cdot \ldots T_{i-1, i} \cdot \left| \begin{array}{c} x_{i}\\ y_{i}\\ z_{i}\\ 1 \end{array} \right|. \end{equation*} | (8) |
Оскільки система координат \((x_i, y_i, z_i)\) прив’язується до \(i-го\) зчленування маніпулятора, то координати рухливої ланки цього зчленування будуть нульовими. Таким чином, маючи трансферну матрицю \(T_{(0,i)}\) можемо розраховувати координати \((x_{(0,i)}, y_{(0,i)}, z_{(0,i)})\) \(i-ї\) ланки маніпулятора в системі координат \((x_0, y_0, z_0)\).

